MedeA Crystals - The Beauty of Periodicity
At-a-Glance
MedeA®[1] Crystals controls all crystal structure information as specified by the lattice vectors in terms of their lengths and the angles between them, the positions of the atoms in the primitive unit cell in terms of their coordinates, and the space-group symmetry.
Key Benefits
- Full control of all crystal structure information
- Symmetry-related atomic positions are automaticlly created
- Straightforward modification of initial magnetic moments and isotope masses
- Freezing of selected atomic coordinates to suppress atomic displacements in structure relaxations, molecular-dynamics simulations, and phonon calculations

M.C. Escher, Lizard, 1942
The unique characteristic, which distinguishes crystals from all other forms of matter, is discrete translational symmetry. This became obvious from the early x-ray diffraction studies, which revealed that most materials form almost perfect periodic arrays at low temperatures [2],[3]. Of course, crystalline periodicity may be viewed as a purely mathematical concept, and in this respect crystals remind you of paintings of M. C. Escher such as that displayed in the figure above.
The mathematical perspective seamlessly leads to the classification of crystals in terms of the well-known 14 Bravais lattices. Each lattice point, i.e. each unit cell of the periodic lattice, may comprise not just a single atom but a complex group of atoms. This is just like the basic unit in the painting by Escher, shown in the above figure, which consists of six lizards, two white, two red, and two black.
On the theoretical side, translational symmetry of a crystal ultimately originates from the corresponding symmetry of the underlying potential generated by the atomic nuclei and seen by the electrons. This led Bloch to formulate his famous theorem, which reduces the problem of describing the electronic states in a macroscopic crystal to that of electronic states in a microscopic unit cell and thus forms the basis for electronic structure calculations using codes like MedeA VASP [4].
MedeA Crystals controls all information about the Bravais lattice and the internal arrangement of the atoms in the unit cell. This is done by the basic graphical user interface displayed in the figure below. It allows you to modify the lattice parameters and angles, to lower the symmetry, e.g. prior to the insertion of symmetry-breaking defects, and to modify the properties of the particular atoms.
The unique characteristic, which distinguishes crystals from all other forms of matter, is discrete translational symmetry.
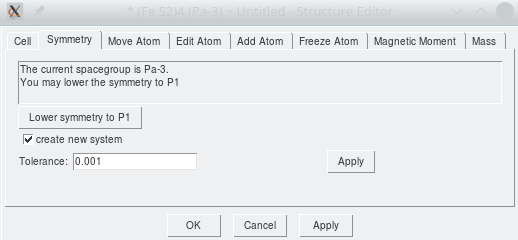
MedeA Crystals Screenshot: Graphical user interface controlling all information about a crystal structure
As an example, the below figure displays the unit cell of FeS2. It crystallizes in a simple cubic lattice with space group Pa-3, which, from a group-theoretical point of view, is exceptional among the 230 space groups [5],[6]. The arrangement of the atoms is characterized by an FeS6 octahedron at the center of the cube, which is rotated away from the Cartesian axes by about 23°, as well as strongly bonded sulfur pairs oriented along the <111> axis.
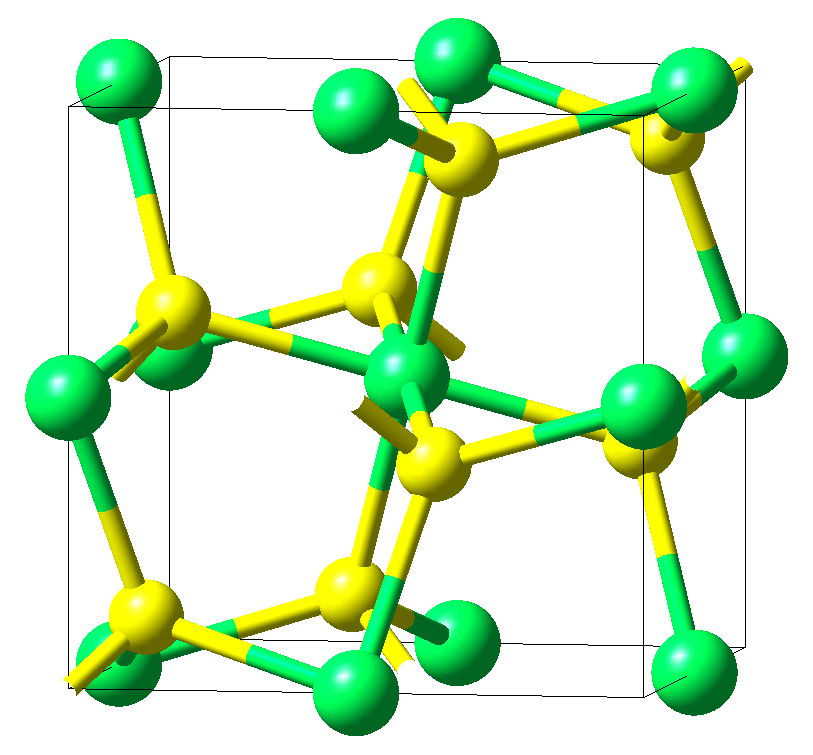
Crystal structure of FeS2as generated using MedeA Crystals
Finally, creation and modification of the crystal structure with MedeA Crystals provides the basis for use with a large number of other tools implemented in the computational MedeA Environment, such as MedeA VASP, the MedeA Interface Builder, and the builder tools for surfaces, supercells, and random substitutions.
Key Features
- An intuitive user interface controls all parameters affecting the crystal structure, such as the lattice parameters and angles, the atomic positions, and the space group
Properties
- Three-dimensional crystal structure as specified by the length of the lattice vectors, the angle between them and the positions of the atoms in Cartesian and fractional coordinates.
- Initial magnetic moments and isotope masses
- Selected suppression of atomic displacements
Required Modules
- MedeA Environment
Find Out More
Learn more about MedeA Crystals Builder from the Materials Design online video tutorial How to Create Vacancies and Substitutions in Bulk Materials.
| [1] | MedeA and Materials Design are registered trademarks of Materials Design, Inc. |
| [2] | W. Friedrich, P. Knipping, and M. Laue, “Interferenz-Erscheinungen bei Röntgenstrahlen”, Ann. Phys. 346, 971 (1912) (DOI) |
| [3] | W. H. Bragg and W. L. Bragg, “The Reflexion of X-rays by Crystals”, Proc. Royal Soc. Lond. A 88, 428 (1913) (DOI) |
| [4] | F. Bloch, “Über die Quantenmechanik der Elektronen in Kristallgittern”, Z. Phys. 52, 555 (1929) (DOI) |
| [5] | C. J. Bradley and A. P. Cracknell, “The Mathematical Theory of Symmetry in Solids”, (Clarendon Press, Oxford 1972) |
| [6] | V. Eyert, K.-H. Höck, S. Fiechter, and H. Tributsch, “Electronic structure of FeS2: The crucial role of electron-lattice interaction”, Phys. Rev. B 57, 6350 (1998). (DOI) |
| download: | pdf |
|---|