MedeA Electronic Transport - When Electrons Get Moving
At-a-Glance
MedeA®[1] Electronic Transport calculates the electronic contributions to the electric and thermal conductivity, the thermoelectric power, and related functions, as based on semiclassical Boltzmann theory.
Key Benefits
- Straightforward set up of the calculation
- Automated distribution over a large number of tasks enables quick calculation
- Accessible range of chemical potentials within a rigid-band scheme
- Straightforward adaptation of fundamental band gap for refined calculation of transport properties
- All quantities displayed as a function of temperature, chemical-potential shift (rigid-band doping), or carrier density
The early attempts at the end of the 19th century to understand the extraordinary transport properties of metals may be well regarded as the outset of solid state theory [2]. In particular, Drude’s theory of metals aimed at describing their high electrical and thermal conductivites [3], which about 50 years before, had been closely tied by the Wiedemann-Franz law. However, it was not before the advent of quantum theory that Sommerfeld was able to devise the first satisfactory theory of the solid state. Even around 100 years later, the calculation of transport properties remains a challenge, which is due in part to the close connection between the electronic and vibrational contributions to transport phenomena.
MedeA Electronic Transport captures the electronic contributions with the help of the semiclassical Boltzmann theory, where the electron dynamics are accounted for by classical equations of motion, while the electronic states and their velocities are taken from first-principles calculations [5] [6] [7].
As an example, the calculated electrical resistivities of several ordered and quasi-disordered structures of Cu1-xAuxalloys as taken from the literature, the cluster expansion as implemented in MedeA UNCLE, and MedeA’s builder of special quasirandom structures (SQS), respectively, and as displayed in the figure below, reveal a striking influence of the microscopic local environment of the atoms on the transport properties. In particular, the ordered structures show systematically reduced electrical resistivities, whereas the resistivities of the disordered structures form a dome, with a maximum at equal concentration of Cu and Au, which is in very good agreement with experimental findings.
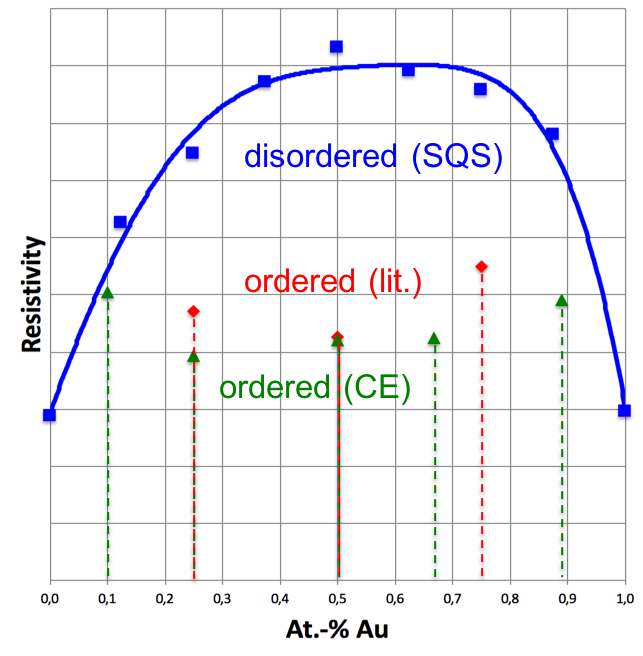
Electrical resistivity of Cu1-xAuxalloys, as calculated using MedeA Electronics.
MedeA Electronic Transport captures the electronic contributions with the help of the semiclassical Boltzmann theory.
Key Features
- MedeA Electronic Transport computes the electronic contributions to the electrical and thermal conductivities, thermoelectric power (Seebeck coefficient), electronic specific heat, Pauli paramagnetic susceptibility, and Hall coefficient
- All quantities can be displayed as a function of temperature, chemical potential (rigid-band doping), or carrier density
- An intuitive user interface allows completely automated setup, execution, and processing of the background jobs required to calculate isosurfaces of the electronic energies and the corresponding effective masses
- MedeA VASP computes electronic eigenvalues
- Full integration into the MedeA Environment allows you to take advantage of MedeA’s robust JobServer and TaskServer Infrastructure
MedeA Electronic Transport Screenshot: Graphical user interface controlling setup of the calculation
Properties
- Electrical conductivity, thermal conductivity
- Thermoelectric power (Seebeck coefficient)
- Electronic specific heat
- Pauli paramagnetic susceptibility
- Hall coefficient
The calculated Seebeck coefficient of Bi2Te3at room temperature is displayed in Figure 3 as a function of doping, as mimicked by rigid shifts of the chemical potential. It agrees well with the experimental values, which for the bulk material range from -250 μV/K (at an n-type doping concentration of 7.4 × 1018 cm-3) to +260 \(\mu V/K\) (at a p-type doping concentration of 4 × 1018 cm-3) [8] [9].
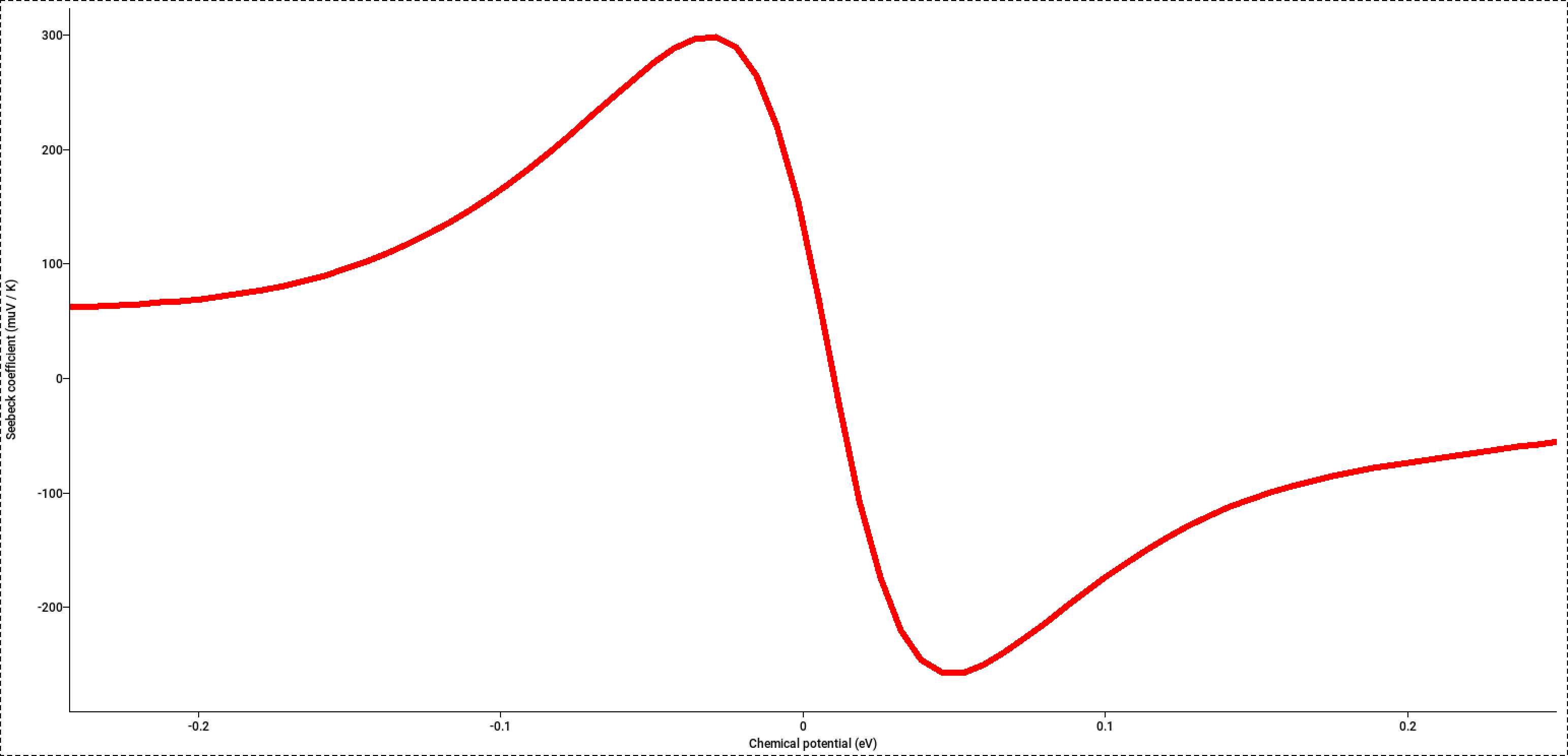
Thermoelectric power of doped Bi2Te3as a function of a simulated rigid band shift mimicking the doping at a temperature of 300 K.
Required Modules
- MedeA Environment
- MedeA VASP
Find Out More
Learn more about MedeA Electronic Transport on Materials Design Application Notes:
- Thermoelectric Properties of Bi2Te3as calculated using MedeA Electronics.
Check out the closely related datasheet on MedeA Special Quasirandom Structures
| [1] | MedeA and Materials Design are registered trademarks of Materials Design, Inc. |
| [2] | N. W. Ashcroft and N. D. Mermin, “Solid State Physics”, (Holt, Rinehart and Winston, New York 1976) |
| [3] | P. Drude, Annalen Phys. 306, 566 (1900) (DOI), ibid. 308, 369 (1900) (DOI) |
| [4] | A. R. Mackintosh, Sci. Am. 209, 110 (1963) (DOI) |
| [5] | T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding, and J. O. Sofo, Phys. Rev. B 68, 125210 (2003) (DOI) |
| [6] | G. K. H. Madsen and D. J. Singh, Comp. Phys. Commun. 175, 67 (2006) (DOI) |
| [7] | V. Eyert, Lect. Notes Phys. 849 (Springer, Berlin Heidelberg 2013) (DOI) |
| [8] | R. Sehr and L. R. Testardi, J. Phys. Chem. Solids 23, 1219 (1962) (DOI) |
| [9] | H. J. Goldsmid, (Springer, New York, 1964) (DOI) |
| download: | pdf |
|---|